Maths Item of the Month
July 2022
The Maths Item of the Month is a monthly problem aimed at teachers and students of GCSE and A level Mathematics. The problems can be used for enrichment, problem solving or as a way to encourage mathematical thinking/proof.
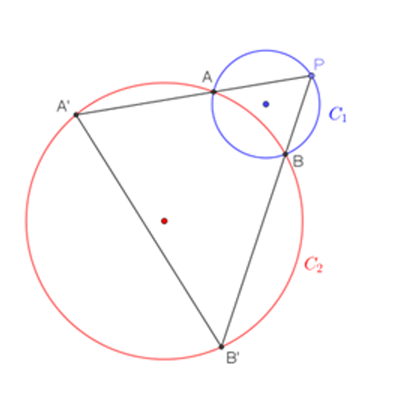
Circle Projection

Looking for more problems?
Check out past editions in our resources listing.
